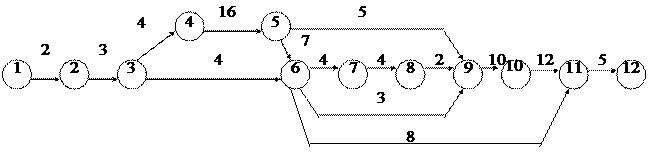Сетевые графики и правила их построения

Сетевой график – это графическое изображение процессов, выполнение которых необходимо для достижения поставленной цели.

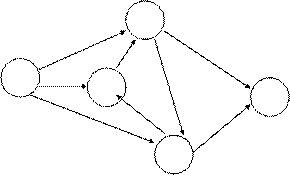
Методы сетевого планирования и управления (СПУ) базируются на теории графов. Графом называется совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами. В экономике обычно используются два вида графов: дерево и сеть. Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины. Сеть — это ориентированный конечный связный граф, имеющий начальную вершину (источник) и конечную вершину (сток). Таким образом, каждый сетевой график представляет собой сеть, состоящую из узлов(вершин) и соединяющих их ориентированных дуг (ребер). Узлы графика называются событиями, а соединяющие их ориентированные дуги — работами. На сетевом графике события изображаются кружками или иными геометрическими фигурами, а соединяющие их работы безразмерными стрелками (безразмерными они называются потому, что длина стрелки не зависит от объема работы, которую она отражает).

Каждому событию сетевого графика приписывают определенный номер (i), а работу, соединяющие события, обозначают индексом (ij). Каждая работа характеризуется своей продолжительностью (длительностью) t(ij). Значение t(ij) в часах или днях проставляют в виде числа над соответствующей стрелкой сетевого графика.

В практике сетевого планирования используют несколько типов работ:

1) реальная работа, производственный процесс, который требует затрат труда, времени, материалов;

2) пассивная работа (ожидание), естественный процесс, который не требует затрат труда и материальных ресурсов, но осуществление которого может происходить лишь в течение определенного периода времени;

3) фиктивная работа (зависимость), которая не требует никаких затрат, но показывает, что какое-то событие не может свершиться ранее другого. При построении графика такие работы обычно обозначают пунктирной линией.

Каждая работа самостоятельно или в сочетании с другими работами заканчивается событиями, которые выражают результаты выполненных работ. В сетевых графиках выделяют следующие события: 1) исходное, 2) промежуточные, 3) завершающее (окончательное). Если событие имеет промежуточный характер, то оно является предпосылкой для начала следующих за ним работ. Считается, что событие не имеет продолжительности и осуществляется мгновенно после выполнения предшествующих ему работ. Исходному событию не предшествуют никакие работы. Оно выражает собой момент наступления условий для начала выполнения всего комплекса работ. Завершающее событие не имеет никаких последующих работ и выражает собой момент окончания всего комплекса работ и достижения намеченной цели.

Взаимосвязанные работы и события сетевого графика образуют пути, которые соединяют исходные и завершающие события, их называют полными. Полный путь на сетевом графике представляет собой последовательность работ по направлению стрелок от исходного до завершающего события. Полный путь максимальной продолжительности называется критическим. Продолжительность критического пути определяет конечный срок выполнения всего комплекса работ и достижения намеченной цели.

Работы, расположенные на критическом пути, называют критическими или напряженными. Все остальные работы считаются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения и сроки свершения событий, не влияя на общую продолжительность выполнения всего комплекса работ.

Правилапостроения сетевого графика.

1. Сеть вычерчивается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.

2. Два соседних события могут соединяться лишь одной работой. При изображении параллельных работ не допускается, чтобы они имели общие начальные и конечные события, так как в этом случае они будут иметь одинаковую нумерацию. Для изображения параллельных работ вводится промежуточное событие и фиктивная работа.

3. В сети не должно быть «тупиков», то есть все события, кроме завершающего, должны иметь последующую работу (тупиками называются промежуточные события, из которых не выходит ни одна работа). Такая ситуация может иметь место, когда данная работа не нужна или какая-либо работа пропущена.

4. В сети не должно быть событий, кроме исходного, которым не предшествует хотя бы одна работа. Такие события называются «хвостовыми». Это может иметь место в случае пропуска предшествующей работы.

5. В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь

Для правильной нумерации событий сетевого графика используют следующую схему действий. Нумерацию начинают из исходного события, которому присваивают номер 0 или 1. Из начального события (1) вычеркивают все исходящие из него работы (ориентированные дуги), и на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию присваивают номер (2). Указанная последовательность действий повторяется до тех пор, пока не буду пронумерованы все события сетевого графика. Если при очередном вычеркивании одновременно возникают два события, не имеющие входящих работ, то номера им присваиваются произвольно. Номер завершающего события должен быть равен количеству событий в сетевом графике.

В процессе построения сетевого графика важное значение имеет определение продолжительности выполнения каждой работы, то есть необходимо дать ей временную оценку. Продолжительность выполнения работ устанавливают либо в соответствии с действующими нормативами, либо на основе экспертных оценок. В первом случае оценки продолжительности называют детерминированными, во втором — стохастическими.

Существуют различные варианты расчета стохастических временных оценок. Рассмотрим некоторые из них. В первом случае устанавливают три вида продолжительности выполнения конкретной работы:

1) максимальный срок, который исходит из наиболее неблагоприятных условий выполнения работы (t_max);

2) минимальный срок, который исходит из наиболее благоприятных условий выполнения работы (t_min);

3) наиболее вероятный срок, исходящий из реальной обеспеченности работы ресурсами и наличия нормальных условий ее выполнения (t_в).

На основе этих оценок рассчитывается ожидаемое время выполнения работы (ее временная оценка) по формуле

. (5.1)

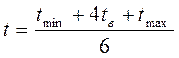
Во втором случае задаются две оценки — минимальная (t_min) и максимальная (t_max). Продолжительность работы в этом случае рассматривается как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Ожидаемое значение данных оценок (t_ож) (при бета-распределении плотности вероятности) оценивается по формуле

. (5.2)

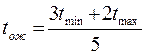
Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии (S 2 )

. (5.3)

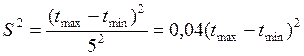
Построение любого сетевого графика начинается с составления полного перечня работ. Затем устанавливается очередность работ, и для каждой конкретной работы определяются непосредственно предшествующие и последующие работы. Для установления границ каждого вида работ используются вопросы: 1) что должно предшествовать данной работе и 2) что должно следовать за данной работой. После составления полного перечня работ, установления их очередности и временных оценок, приступают непосредственно к разработке и составлению сетевого графика.

Рассмотрим в качестве примера программу строительства здания склада. Перечень операций, их последовательность и временную продолжительность оформим таблицей.

Перечень работ сетевого графика

Операция	Описание операции	Непосредственно предшествующая операция	Продолжитель-ность, дн.
А	Расчистка строительной площадки	—
Б	Выемка котлована под фундамент	А
В	Уклада фундаментных блоков	Б
Г	Прокладка наружных инженерных сетей	Б
Д	Сооружение каркаса здания	В
Е	Кровельные работы	Д
Ж	Внутренние сантехнические работы	Г, Е
З	Настилка полов	Ж
И	Установка дверных и оконных рам	Д
К	Теплоизоляция перекрытий	Е
Л	Прокладка электропроводной сети	З
М	Штукатурка стен и потолков	И, К, Л
Н	Внутренняя отделка	М
О	Наружная отделка	Е
П	Благоустройство территории	Н, О

Построенный на основании данных табл. 5.1 предварительный сетевой график выполнения работ выглядит следующим образом (рис. 5.1).

Рис. 5.1. Предварительный сетевой график

Ниже приведен тот же самый график строительства складского здания, пронумерованный и с проставленными временными оценками работ (рис. 5.2).

Рис. 5.2. Окончательный вариант сетевого графика

Исполнительная документация

Графики

Графики разные по строительству скачать :

Примеры графиков производства работ:

1 График производства земляных работ, пример скачать jpg , скачать rar

2 График производства работ по строительству школы, пример скачать doc

3 График производства работ по объекту: Центральный тепловой пункт ЦТП, пример скачать xls , скачать zip

4 График производства работ на комплекс работ по устройству наружного освещения, кабельной сети и декоративной подсветки, пример скачать xls , скачать zip

5 График производства работ на реконструкцию, пример скачать xls , скачать zip

Примеры календарных графиков:

1 Календарный график производства работ, календарный график движения рабочей силы, машин и механизмов на прокладку полиэтиленовых труб, бланк (в формате Компас V15.1) скачать frw

2 Календарный график выполнения работ по объекту, пример скачать xls.

3 Календарный график, пример скачать zip, скачать pdf.

4 Календарный план производства работ на тепловые сети, пример скачать zip, скачать doc.

5 Календарный план производства работ на установку опор ВОЛС, пример скачать zip, скачать doc.

6 Месячно-суточный график выполнения работ, пример скачать xls, скачать zip

Примеры прочих графиков:

1 График подготовки и сдачи исполнительной технической документации ИТД, пример скачать xls , скачать zip

2 График потребности в рабочих кадрах и основных строительных машинах, пример скачать xls , скачать zip

3 График поступления на объект строительных конструкций, изделий и материалов, пример скачать xls , скачать zip

4 График поставок материалов и оборудования, пример скачать doc , скачать zip

5 График движения рабочей силы, пример скачать xls , скачать zip

5а График движения персонала на строительстве, пример скачать xls , скачать zip

6 График выполнения СМР, пример скачать pdf , скачать zip

7 График кирпичной кладки, пример скачать xls, скачать zip

8 Плановый график расстановки специалистов подрядной организации, пример скачать xls, скачать zip

9 Фактический график расстановки специалистов подрядной организации, пример скачать xls, скачать zip

10 График (табель) учёта фактически отработанных дней специалистов подрядной организации, пример скачать xls+приложение, скачать zip

Смотрите состав исполнительной в разделе: «Состав исполнительной»

Скачивайте акты, протокола и другое в разделе: «Акты и прочее»

Скачивайте полезные книги, ГОСТы, СнИПы в разделе: «ГОСТы и книги«

Управление проектами для «чайников».

Простои пример применения сетевого графика.

Рассмотрим применение сетевого графика на примере организации пикника. (Я, в общем-то, не настаиваю, чтобы вы каждый пикник планировали с помощью сетевого графика, но этот пример покажет основные приемы и возможности.).

В пятницу вечером, после напряженной недели, вы с подругой обсуждаете, как с максимальной пользой провести выходные. Прогноз обещает хорошую погоду, и вы решаете с утра отправиться на пикник на одно из двух ближайших озер. Чтобы как можно лучше организовать пикник и развлечься, вы решили составить сетевой график.

В табл. 4 5 представлены семь работ, которые, как вы считаете, необходимо выполнить, чтобы подготовить пикник и добраться до озера.

Таблица 4.5. Список мероприятий по организации пикника на озере.

Номер работы	Наименование работы	Исполнитель	Продолжительность (в мин.)
1	Погрузить вещи в машину	Вы и подруга	5
2	Получить деньги в банке	Вы	5
3	Приготовить сэндвичи с яйцом	Подруга	10
4	Поехать на озеро	Вы и подруга	30
5	Выбрать озеро	Вы и подруга	2
6	Заправить машину бензином	Вы	10
7	Сварить яйца (для сэндвичей)	Подруга	10

Кроме того, вы соблюдаете следующие условия.

• Все работы начинаются в субботу в 8:00 утра у вас дома. До этого времени нельзя ничего делать.

• Необходимо выполнить все работы по данному проекту.

• Вы договорились не менять исполнителей запланированных работ.

• Оба озера находятся в противоположных направлениях от вашего дома, поэтому прежде, чем отправляться в путь, следует решить, на какое из них ехать.

Вначале вы решаете, в каком порядке будете выполнять все эти работы. Другими словами, вам нужно определить для каждой работы непосредственно предшествующую. Необходимо учесть такие зависимости.

• Подруга должна сварить яйца, прежде чем готовить сэндвичи.

• Вы вместе должны решить, на какое озеро ехать, прежде чем отправиться в путь.

В каком порядке выполнять остальные работы, зависит от вашего желания. Например, вы приняли такой порядок.

• В первую очередь вы вместе решаете, на какое озеро ехать.

• Приняв решение насчет озера, вы отправляетесь в банк за деньгами.

• Получив деньги в банке, вы заправляете машину.

• После принятия совместного решения об озере подруга начинает варить яйца.

• После того как яйца сварились, подруга делает сэндвичи.

• После того как вы вернулись с заправки и подруга приготовила сэндвичи, грузите вещи в машину.

• После того как вы оба загрузили машину, отправляетесь к озеру.

Табл. 4.6 иллюстрирует последовательность работ, которую вы определили.

Таблица 4.6. Последовательность работ для организации пикника.

Номер работы	Описание работы	Непосредственно предшествующая работа
1	Погрузить вещи в машину	3, 6
2	Получить деньги в банке	5
3	Приготовить сэндвичи с яйцом	7
4	Поехать на озеро	1
5	Выбрать озеро	Нет

6	Заправить машину бензином	2
7	Сварить яйца (для сэндвичей)	5

Чтобы построить сетевой график в соответствии с этой таблицей, выполните следующие действия.

1. Начните проект с события «Начало».

2. Затем определите все работы, которые не имеют предшествующих. К их выполнению можно приступать стразу с момента начала проекта.

В нашем случае это единственная работа 5.

3. Начинаем рисовать сетевой график (рис. 4.5).

Определите все работы, для которых работа 5 является непосредственно предшествующей.

Рис 4.5. Начало построения сетевого графика организации пикника.

4. Из табл. 4.6 видно, что таких две: работа 2 и работа 7. Изобразите их в виде прямоугольников и проведите к ним стрелки от работы 5.

Продолжайте строить график по тому же принципу.

Для работы 6 предшествующей будет работа 2, а для работы 3 — работа 7. На данном этапе график примет вид, как на рис 4.6.

Из таблицы видно, что работе 1 предшествуют две работы: работа 3 и работа 6, а работе 4 — только работа 1. И наконец, от работы 4 идет стрелка к событию «Конец».

Рис. 4.6. Продолжение построения сетевого графика организация пикника.

На рис. 4.7 показан сетевой график в завершенном виде.

Рис. 4.7. Окончательный вид сетевого графика для организации пикника.

Теперь рассмотрим несколько важных вопросов. Во-первых, сколько времени вам потребуется, чтобы собраться и добраться до озера?

• Верхний путь, включающий работы 2 и 6, — 15 минут.

• Нижний путь, включающий работы 7 и 3, составляет 20 минут.

• Самый длинный в графике — критический путь, он включает работы 5, 7, 3, 1 и 4. Его продолжительность — 57 минут. Именно столько вам понадобится, чтобы добраться до озера, если следовать этому сетевому графику.

Можно ли задержать выполнение некоторых работ и все же уложиться в 57 минут? Если да, то каких?

• Верхний путь, включающий работы 2 и 6, — не критический.

• Из сетевого графика следует, что поскольку работы 5, 7, 3, 1 и 4 находятся на критическом пути, они не могут быть задержаны ни в коем случае.

• Однако работы 2 и 6 можно выполнять одновременно с работами 7 и 3. Работы 7 и 3 занимают 20 минут, в то время как работы 2 и 6 — 15 минут. Поэтому работы 2 и 6 имеют резерв времени в 5 минут.

На рис. 4.8 представлен тот же сетевой график, но в форме «события-работы». Событие А эквивалентно событию «Начало», а событие I эквивалентно событию «Конец».

Рис. 4.8. Окончательный вид сетевого графика для организации пикника в форме «события-работы «.

Представленные на рис. 4.8 события пока не имеют названий. Вы можете дать их, например:

• событие В, конец работы 5 («Выбрать озеро»), можно назвать «Решение принято»;

• событие С, конец работы 2 («Получить деньги»), можно назвать «Деньги получены». И так далее.

Элементарным называется событие, которое завершает одну работу. Определение элементарных событий в конце всех работ на сетевом графике типа «события-работы» упрощает отслеживание выполнения работ. Если работа 1 имеет несколько предшествующих, то вместо того чтобы проводить несколько стрелок к событию, после которого начинается работа 1, выполните следующее:

• закончите каждую предшествующую работу элементарным событием;

• соедините их стрелками со следующим элементарным событием, от которого начнется работа 1. Стрелки в этом случае будут означать фиктивные работы.

Это показано на рис. 4.8. Вы должны закончить работу 6 «Заправить машину», а ваша подруга работу 3 «Приготовить сэндвичи» до того, как вы оба начнете грузить вещи в машину. Вместо того чтобы вести стрелки прямо к событию G, закончите работу 6 событием D «Машина заправлена», а работу 3 событием F «Сэндвичи приготовлены». Затем обозначьте фиктивные работы стрелками от событий D и F к событию G, которое можно назвать «Готовы к загрузке машины».